Functions in mathematics can be compared to the operations of a vending (soda) machine. When you put in a certain amount of money, you can choose different types of sodas. Similarly, for functions, we input different numbers and we see new numbers as the result. Domain and range are the principal aspects of functions. You can use quarters and one-dollar bills to purchase a soda.
The machine will not provide you any flavor of the soda if pennies are input. Hence, the domain denotes the inputs we can have here, that is, quarters and one-dollar bills. No matter what amount you give, you won’t get a cheeseburger from a soda machine. Thus, the range is the possible outputs we can have here, that is, the flavors of soda in the machine. Let us learn to find the domain and range of a given function, and also graph them.
Table of Contents
What are Domain and Range?
Domain and Range are the components of a function. The domain is the set of all the input values of a function and range is the potential output given by the function. Domain→ Function →Range. If there exists a function f: A →B such that each element of A is mapped to elements in B, then A is the domain and B is the co-domain. The image of an element ‘a’ under a relation R is given by ‘b’, where (a,b) ∈ R. The range of the function is the set of images. The domain and range of a function is denoted in general as follows: Domain(f) = {x ∈ R} and range(f)={f(x) : x ∈ domain(f)}
The domain and range of this function f(x) = 2x is given as domain D ={x ∈ N } , range R = {(y): y = 2x}
The domain of a Function
A domain refers to “all the values” that go into a function. The domain of a function is the set of all possible inputs for the function. Consider this box as a function f(x) = 2x. Inputting the values x = {1,2,3,4,…}, the domain is simply the set of natural numbers and the output values are called the range.
Range of a Function
The range of a function is the set of all its outputs. Example: Let us consider the function f: A→ B, where f(x) = 2x and A and B = {set of natural numbers}. Here we say A is the domain and B is the co-domain. Then the output of this function becomes the range. The range = {set of even natural numbers}. The elements of the domain are called pre-images and the elements of the co-domain which are mapped are called the images. Here, the range of the function f is the set of all images of the elements of the domain (or) the set of all the outputs of the function.
How To Find Domain And Range?
Suppose X = {1, 2, 3, 4, 5}, f: X → Y, where R = {(x,y) : y = x+1}.
Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
Range = the output values of the function = {2, 3, 4, 5, 6}
and the co-domain = Y = {2, 3, 4, 5, 6}
Let’s understand the domain and range of some special functions taking different types of functions into consideration.
Domain and Range of Exponential Functions
The function y = ax, a ≥ 0 is defined for all real numbers. Hence, the domain of the exponential function is the whole real line. The exponential function ever results in a positive value. Thus, the range of the exponential function is of the form y= |ax+b| is y ∈ R , {y > 0}. Domain = R, Range = (0, ∞)
Example: Look at the graph of this function f: 2x
Observe that the value of the function is closer to 0 as x tends to ∞ but it will never attain the value 0. The domain and range of an exponential function are provided as follows:
- Domain: The domain of the function is the set R.
- Range: The exponential function always results in positive real values.
Domain and Range of Trigonometric Functions
Look at the graph of the sine function and cosine function. See that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.
The domain and range of a trigonometry function are given as follows
Domain: The domain of the functions is the set R.
Range: The range of the functions is [-1, 1]
Domain and Range of an Absolute Value Function
The function y=|ax+b| is defined for all real numbers. So, the domain of the absolute value function is the set of all real numbers. The absolute value of a number always results in a non-negative value. Thus, the range of an absolute value function of the form y= |ax+b| is y ∈ R | y ≥ 0. The domain and range of an absolute value function are given as follows
Domain = R, Range = (0, ∞)
Example: |6-x|
- Domain: The domain of the function is the set R
- Range: We already know that the absolute value function results in a non-negative value always.
|6-x| ≥ 0
6 – x ≥ 0
x ≤ 6
Domain and Range of a Square Root Function
The function y= √(ax+b) is defined only for x ≥ -b/a
Thus, the domain of the square root function is the set of all real numbers greater than or equal to b/a. We know that the square root of something ever results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. The domain and range of a square root function are given as: Domain = (-b/a,∞), Range = [0,∞]
Example: y= 2- √(-3x+2)
Domain: A square root function is set only when the value inside it is a non-negative number. So for a domain,
-3x+2 ≥ 0
-3x ≥ -2
x ≤ 2/3
Range: We already know that the square root function results in a non-negative value always.
√(-3x+2)≥ 0
Multiply -1 on both sides
-√(-3x+2) ≤ 0
Adding 2 on both sides
2-√(-3x+2)≤ 2
y≤ 2
Graphs of Domain and Range
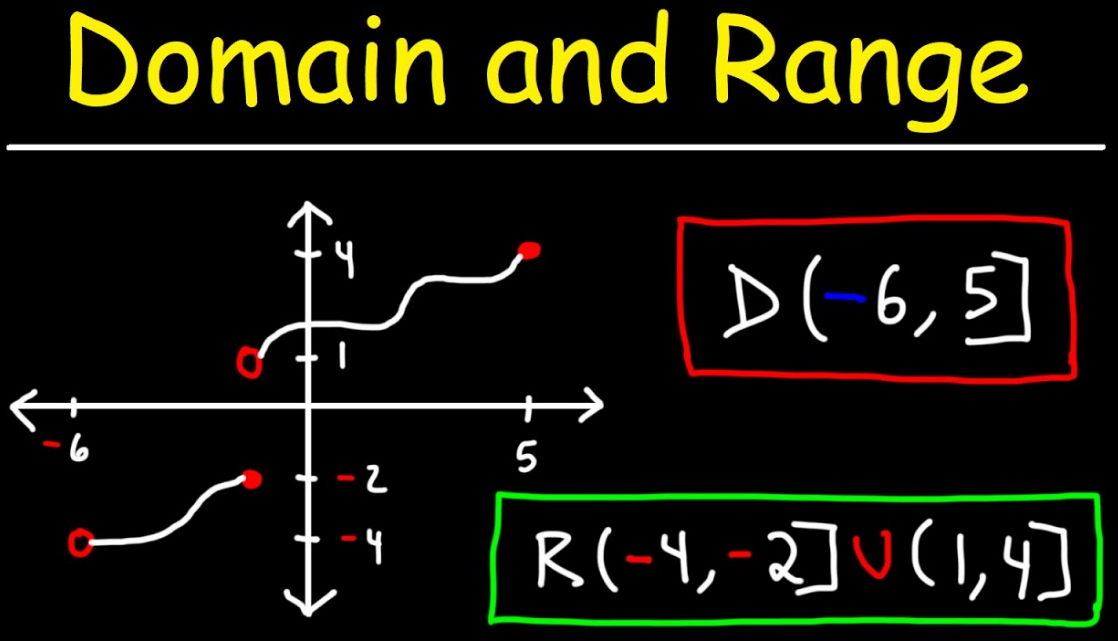
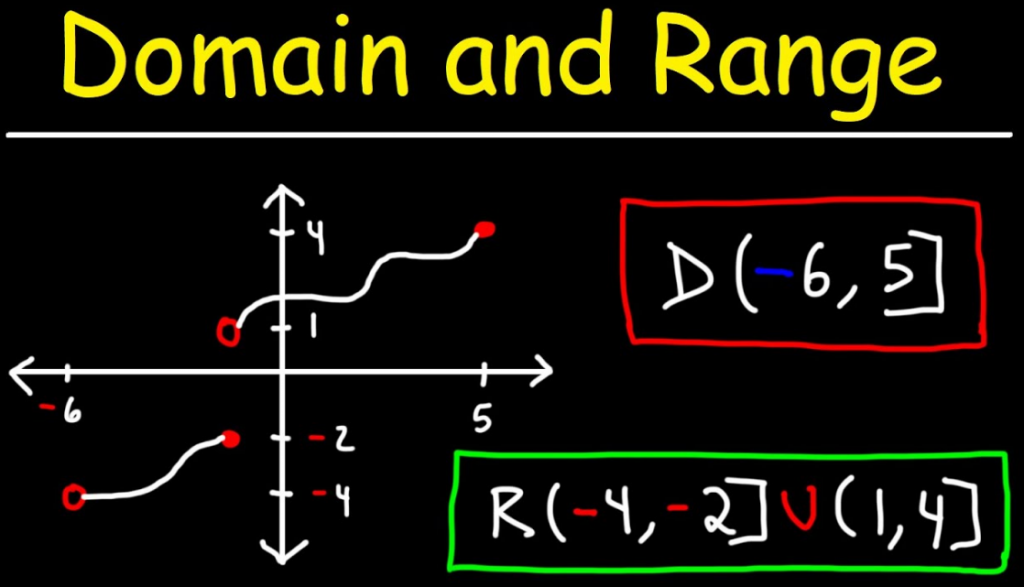
Another way to know the domain and range of functions is by using graphs. The domain leads to the set of possible input values. The domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values shown on the y-axis. The most apparent method to find the range of a function is by graphing it and looking for the y-values covered by the graph. To see the range of a quadratic function, it is sufficient to see if it has a maximum or minimum value. The maximum/minimum value of a quadratic function is the y-coordinate of its vertex. To see the domain of the rational function, set the denominator as 0 and solve for the variable. The domain is denoted by all the values from left to right along the x-axis and the range is given by the span of the graph from the top to the bottom.
Important Notes
- The domain and range of a function is the set of all possible inputs and outputs of a function sequentially.
- The domain and range of a function y = f(x) is given as domain= {x ,x∈R }, range= {f(x), x∈Domain}.
- The domain and range of any function can be obtained algebraically or graphically.
FAQs
The domain and range in a function are the set of all the inputs and outputs a function can give respectively. The domain and range are important aspects of a function. The domain takes all the possible input values from the set of real numbers and the range takes all the output values of the function.
We write the domain and range as the set of all the inputs a function can take and the outputs of the functions respectively. The domain and range are written from the smaller values to the larger values. The domain is written from left to right and the range is written from the top of the graph to the bottom.
The natural domain and range of a function are all the possible input values and the output values of the function respectively. Domain(f) = {x∈R} and range(f)={f(x):x ∈ domain(f)}.
Let the constant function be f(x)=k. The domain of a constant function is given by R, that is, the set of real numbers. The range of a constant function is given by the singleton set, {k}. The domain and range of a constant function are given as domain = x∈R and range = {k}, which is a singleton set.