How to find arc length? A part of a curve or a part of a circumference of a circle is named Arc. All of them have a curve in their pattern. The curved portion of these things is mathematically called an arc. Arc length is better defined as the distance along the part of the circumference of any circle or any curve (arc).
Any distance along the curved line that makes up the arc is acknowledged as the arc length. The length of an arc is longer than any straight line distance within its endpoints (a chord).
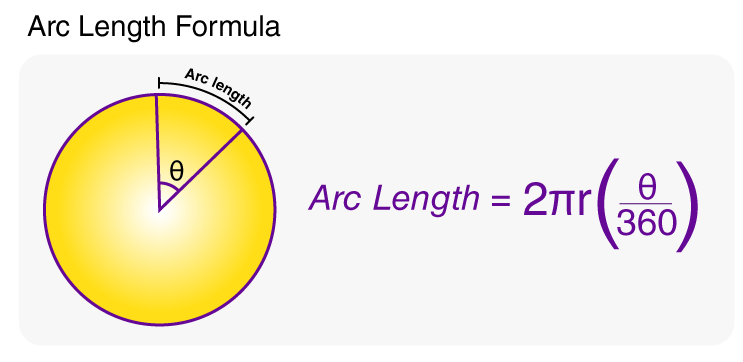
Table of Contents
What is Arc Length?
Thearc length is determined as the interspace between the two points along a section of a curve. An arc of a circle is any portion of the circumference. The angle subtended by an arc at any point is the angle made between the two line segments joining that point to the end-points of the arc. For instance, in the circle shown below, OP is the arc of the circle with center Q. The arc length of this arc OP is performed as L.
Arc Length Formula
The length of an arc can be measured using different formulas, based on the unit of the central angle of the arc. The dimensions of the central angle can be given in degrees or radians, and accordingly, we calculate the arc length of a circle. For a circle, the arc length formula is θ times the radius of a circle.
The arc length formula in radians can be represented as, arc length = θ × r, when θ is in radian. Arc Length = θ × (π/180) × r, where θ is in degree, where,
- L = Length of an Arc
- θ = Central angle of Arc
- r = Radius of the circle
Arc Length Formula in Radians
The arc length of a circle can be determined using different formulas, based on the unit of the center angle of the arc. The arc length formula in radians can be shown as,
Arc Length = θ × r
where,
- L = Arc Length
- θ = Center angle of the arc in radians
- r = Radius of the circle
How to Find Arc Length of a Curve?
The arc length of an arc of a circle can be measured using different methods and formulas based on the given data. Some important cases are given below,
- find arc length with the radius and central angle
- find arc length without the radius
- find arc length without the central angle
How to See Arc Length With the Radius and Central Angle?
The arc length of a circle can be determined with the radius and central angle using the arc length formula,
- Length of an Arc = θ × r, where θ is in radian.
- Length of an Arc = θ × (π/180) × r, where θ is in degree.
How to Find Arc Length Without the Radius?
The arc length of a circle can be calculated without the radius utilizing:
Central angle and the sector area:
- Multiply the sector area by 2 and further, share the result by the central angle in radians.
- Find the square root of the result of the division.
- Multiply this concerned root by the central angle again to get the arc length.
- The units of this determined arc length will be the square root of the sector area units.
Example: Determine the arc length of a curve with sector area 25 square units and the central angle as 2 radians.
We have,
Sector area = 25 units
Central angle = 2 radians
- Step 1: Sector area × 2 = 25 × 2 = 50
- Step 2: 50/central angle = 50/2 = 25
- Step 3: √25 = 5
- Step 4: 5 × central angle = 5 × 2 = 10 units
Thus, arc length = 10 units
Central angle and the chord length:
- Divide the central angle in radians by 2 and more, perform the sine function on it.
- Divide the given chord length by twice the result of step 1. This calculation presents you the radius as result.
- Multiply the radius by the central angle to see the arc length.
Example: Determine the arc length of a curve, whose endpoints touch a chord of the circle measuring 5 units. The central angle subtended by the arc is 2 radians.
We have,
Chord length = 5 units
Central angle = 2 radians
- Step 1: Central angle/2 = 2/2 = 1
- Step 2: Sin(1) = 0.841
- Step 3: Chord length/ (2 × 0.841) = 5/ 1.682 = 2.973 units = radius
- Step 4: Arc length = radius × central angle = 2.973 × 2 = 5.946 units
Thus, arc length = 5.946 units
How to See Arc Length Without the Central Angle?
The arc length of a circle can be determined without the angle using:
Radius and the sector area:
- Multiply the sector area by 2.
- Then divide the result by the radius squared (the units should be the same) to see the central angle in radians.
- Multiply the central angle by the radius to see the arc length.
Example: Determine the arc length of a curve with sector area 25 square units and radius as 2 units.
We have,
Sector area = 25 units
Central angle = 2 units
- Step 1: Sector area × 2 = 25 × 2 = 50
- Step 2: 50/radius2 = 50/4 = 12.5 = central angle(rad)
- Step 3: Arc length = radius × central angle = 2 × 12.5 = 25 units
Thus, arc length = 25 units
Radius and chord length:
- Divide the chord length by twice the supplied radius.
- Get the inverse sine of the obtained result.
- Double the result of the inverse sine to get the central angle in radians.
- Multiply the central angle by the radius to see the arc length.
Example: Determine the arc length of a curve, whose endpoints touch a chord of the circle measuring 5 units. The radius of the circle is 2 units.
We have,
Chord length = 5 units
Central angle = 2 units
- Step 1: Chord length/(2 × radius) = 5/(2 × 2) = 1.25
- Step 2: Sin-1(1.25) = 0.949
- Step 3: Central angle = 2 × 0.949 = 1.898 radians
- Step 4: Arc length = radius × central angle = 2 × 1.898 = 3.796 units
Thus, arc length = 3.796 units
FAQs
A circle’s arc length is defined as the distance between two points along a section of a curve. Circumferences of circles are defined as arcs. In any given point, the angle subtended by an arc is that formed by two line segments joining that point to the end-points of the arc.
The arc length can be calculated when the central angle is given in radians using the formula: Arc Length = θ × r when θ is in radians.
L = Arc Length
θ = Center angle of the arc
r = Radius of the circle
No, arc length cannot be in radians. Distances cannot be measured in radians, so can’t be measured in degrees. Angles subtended at the center can be expressed in radians, degrees, or arcsecs.
When arc length is presented with central angle θ then the circumference is calculated as Arc Length (L)/Circumference = θ/360º.
A major arc of a circle is larger than a semicircle. It is measured as larger than 180°. Using the formula ℓ = rθ we can obtain the length of an arc of a circle, where θ is in radians.
