How to find the area of a polygon? The area of a polygon is defined as the area that is enclosed by the boundary of the polygon. In other words, we say that the region that is occupied by any polygon gives its area. In this lesson, we will learn to determine the area of polygons and find the difference between the perimeter and area of polygons in detail.
Table of Contents
What is the Area of a Polygon?
The definition of the area of a polygon is the measure of the area that is enclosed by it. As polygons are closed plane shapes, thus, the area of a polygon is the space that is occupied by it in a two-dimensional plane. The unit of the area of any polygon is always expressed in square units. Observe the following figure which shows the area of a polygon on a two-dimensional plane.
Area of Polygon Formulas
A polygon can be categorized as a regular or an irregular polygon based on the length of its sides. Thus, this differentiation also brings a difference in the calculation of the area of polygons. The area of some commonly known polygons is given as:
- Area of triangle = (1/2) × base × height
We can also find the area of a triangle if the length of its sides is known by using Heron’s formula which is, Area = \(\sqrt{s(s-a)(s-b)(s-c)}\), where s = Perimeter/2 = (a + b + c)/2, a, b, and c are the length of its sides. - Area of rectangle = length × width
- Area of parallelogram = base × height
- Area of trapezium = (1/2) × (sum of lengths of its parallel sides or bases) × height
- Area of rhombus = (1/2) × (product of diagonals)
In order to calculate the area of a polygon, it must be first known whether the given polygon is a regular polygon or an irregular polygon.
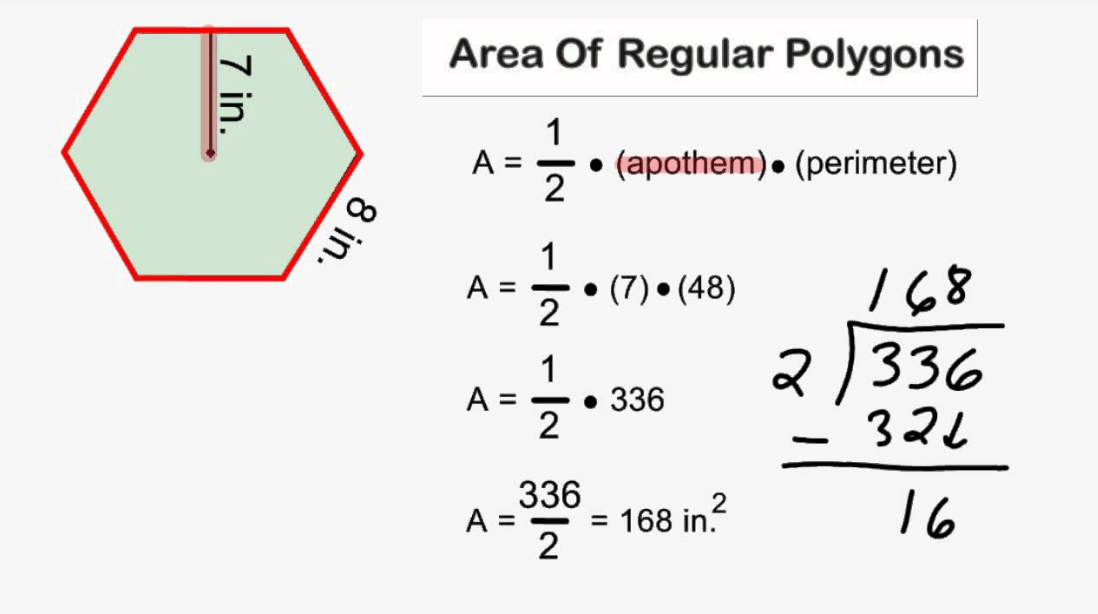
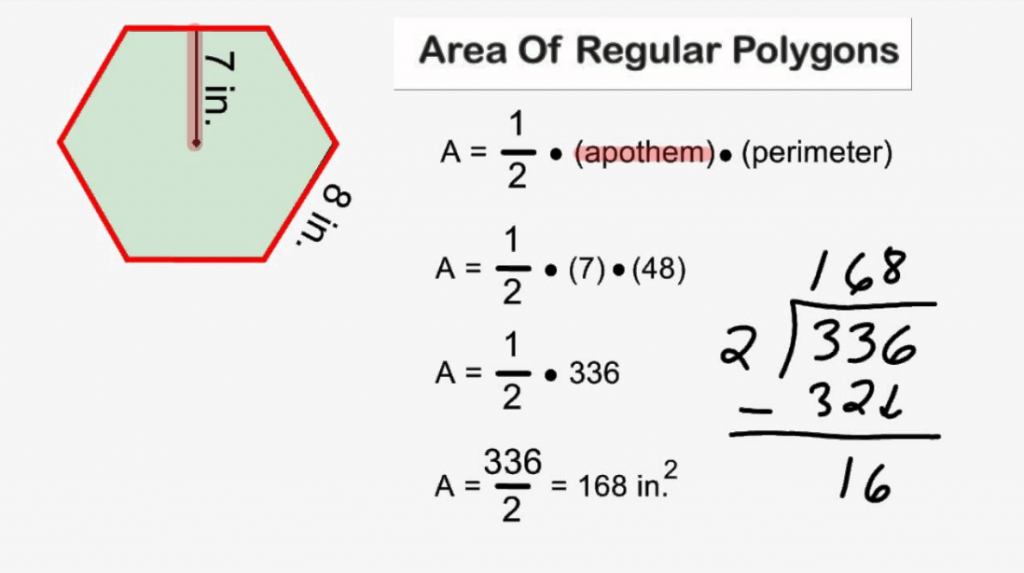
Area of Regular Polygons
A regular polygon is a polygon that has equal sides and equal angles. Thus, the technique to calculate the value of the area of regular polygons is based on the formulas associated with each polygon.
In order to determine the area of a regular polygon, if the number of its sides are known, is given by:
- Area of regular polygon = (number of sides × length of one side × apothem)/2, where the length of apothem is given as the \(\dfrac{l}{2\tan(\dfrac{180}{n})}\), where l is the side length and n is the number of sides of the regular polygon.
- In terms of the perimeter of a regular polygon, the area of a regular polygon is given as, Area = (Perimeter × apothem)/2, in which perimeter = number of sides × length of one side
Example: Find the area of a regular pentagon whose side is 7 inches long.
Solution: Given the length of one side = 7 inches.
Hence, the area of the regular pentagon is given as A = \(\dfrac{1}{4} × \sqrt{5(5+2√5)} × (side)^2\)
⇒ A = \(\dfrac{1}{4} × \sqrt{5(5+2√5)} × (7)^2\)
⇒ A = 84.3 square inches
Thus, the area of the regular pentagon is 84.3 square inches.
Area of Irregular Polygons
An irregular polygon is a plane closed shape that does not have equal sides and equal angles. Thus, in order to calculate the area of irregular polygons, we split the irregular polygon into a set of regular polygons such that the formulas for their areas are known.
Area of Polygons with Coordinates
The area of polygons with coordinates can be found using the following steps:
- Step 1: First we find the distance between all the points using the distance formula, D = \(\sqrt {\left( {x_2 – x_1 } \right)^2 + \left( {y_2 – y_1 } \right)^2 }\)
- Step 2: Once, the dimensions of the polygons are known find whether the given polygon is a regular polygon or not.
- Step 3: If the polygon is a regular polygon we use the formula, area of regular polygon = (number of sides × length of one side × apothem)/2, where the length of apothem is given as the (length of one side)/(2 ×(tan(180°/number of sides))). If the polygon is an irregular polygon, it is to be divided into several regular polygons to find the area.
Example: What is the area of the polygon formed by the coordinates A(0,0), B(0, 2), C(2, 2), and D(2, 0)?
Solution: On plotting the coordinates A(0,0), B(0, 2), C(2, 2), and D(2, 0) on an XY plane and joining the dots we get,
It can be seen, the obtained figure shows a four-sided polygon. In order to understand whether it is a regular polygon or not, we find the distance between all the points.
Length of AB = \(\sqrt{({0 – 0})^2 + ({2 – 0})^2}\) = 2 units
Length of BC = \(\sqrt{({2 – 0})^2 + ({2 – 2})^2}\) = 2 units
Length of CD = \(\sqrt{({2 – 2})^2 + ({0 – 2})^2}\) = 2 units
Length of DA = \(\sqrt{({0 – 2})^2 + ({0 – 0})^2}\) = 2 units
Now that we know the length of all sides of the given polygon is the same, it shows, it is a square. Thus, the area of the polygon ABCD is given as A = (length)2 = (2)2 = 4 square units.
Hence, the area of the polygon with coordinates (0,0), (0, 2), (2, 2), and (2, 0) is 4 square units.
Important Notes
- If the length of one side is given, it is possible to find the area of the regular polygon by finding apothem.
- Apothem falls on the midpoint of a side at the right angle dividing it into two equal parts.
- An Equilateral triangle is a regular polygon with 3 sides, while a square is a regular polygon with 4 sides. Hence, they are not prefixed as regular ahead of the shape name.
FAQs
The space enclosed by any polygon in a two-dimensional plane is defined as the area of the polygon. We write the unit of area of a polygon in square units where the unit can be SI units like meters or centimeters, etc. or USCS units (inches or feet, etc).
The area of a polygon can be calculated by understanding whether the given polygon is a regular polygon or an irregular polygon. The steps to calculate the area of polygons are:
Step 1: Find whether the given polygon is a regular polygon or not.
Step 2: If it is a regular polygon or has a standard formula of calculation, use it to determine the value with all the given dimensions of the polygon, otherwise, the area of the polygon can be calculated by dividing it into a set of regular polygons whose area can be added to get the area of the required polygon.
If the number of sides of a polygon is given, the area of the polygon can be calculated with the help of the formula, Area = [(L2 n)/4 tan(180/n)]; where L is the length of its side and ‘n’ is the number of sides of the polygon.
The perimeter of a polygon is the total length of its boundary, whereas, the area of a polygon is the region occupied by it. The perimeter of a polygon is obtained by adding the length of all its sides while the area of a polygon is obtained by using the required formula depending upon whether the given polygon is a regular polygon or not.
The unit of the perimeter of a polygon is always given in linear units as it is one-dimensional while the unit of the area of a polygon is always given in square units because the area is a two-dimensional concept.
In order to calculate the value of the area of an irregular polygon we use the following steps:
Step 1: Divide the given polygon into smaller sections forming different regular or known polygons.
Step 2: Find the area of each section individually.
Step 3: Add the area of each section to obtain the area of the given irregular polygon.