Interval notation is a method to represent an interval on a number line. In other words, it is a way of writing subsets of the real number line. An interval comprises the numbers lying between two specific given numbers. For example, the set of numbers x satisfying 0 ≤ x ≤ 5 is an interval that contains 0, 5, and all numbers between 0 and 5.
Let us understand the interval notation and different types of intervals in detail using solved examples.
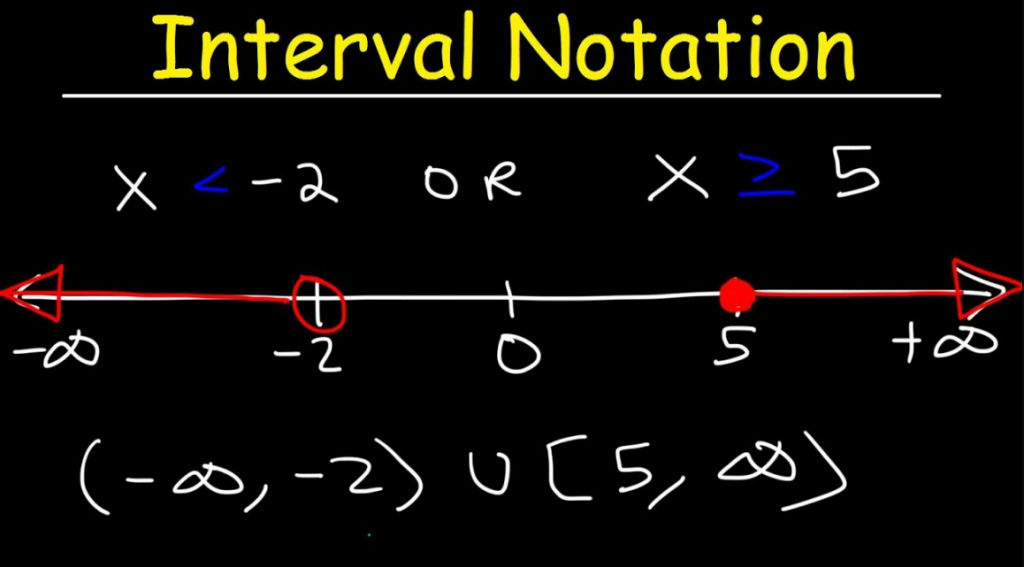
Table of Contents
What is Interval Notation?
Interval Notation is a way of expressing a subset of real numbers by the numbers that bound them. We can use this notation to represent inequalities. We know an interval expressed as 1 < x < 5 denotes a set of numbers lying between 1 and 5.
Examples of Interval Notation
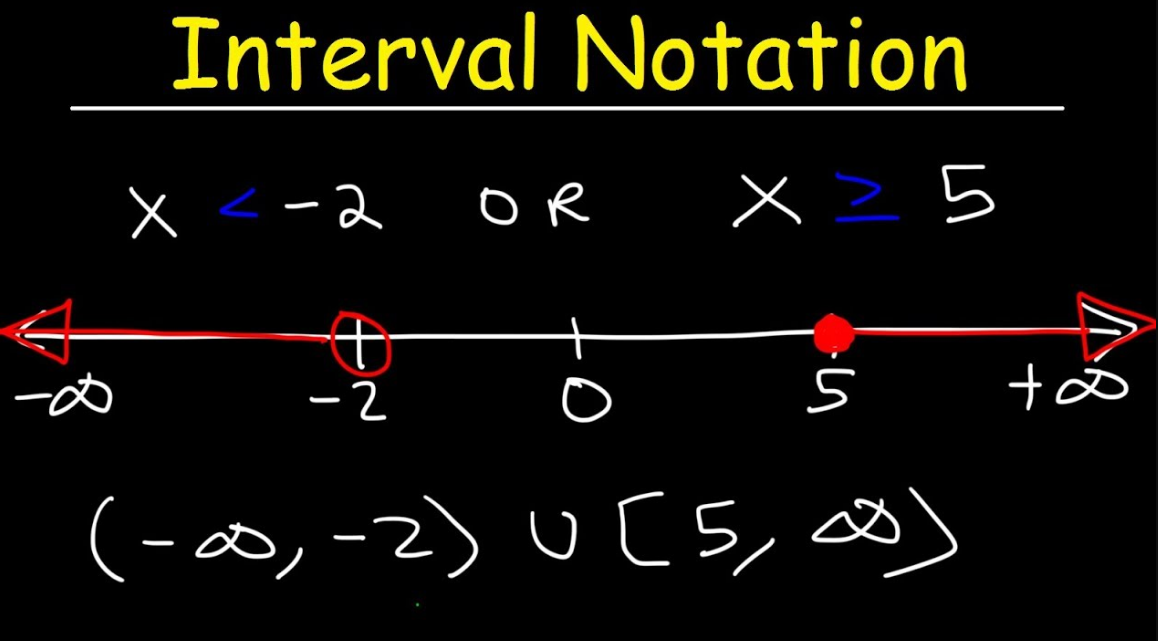
Suppose we want to express the set of real numbers {x |-2 < x < 5} using an interval. This can be expressed as interval notation (-2, 5).
The set of real numbers can be expressed as (-∞, ∞).
Different Types Of Intervals
Intervals can be classified based on the numbers the set comprises. Some sets include the endpoints specified in the notation, while others might partially or not include the endpoints. In general, there are three types of intervals:
- Open Interval
- Closed Interval
- Half-Open Interval
Open Interval
This type of interval does not include the endpoints of the inequality. For example, the set {x | -3 < x < 1} does not include the endpoints, -3 and 1. This is expressed using open interval notation: (-3, 1).
Closed Interval
This type of interval includes the endpoints of the inequality. For example, the set {x | -3 ≤ x ≤ 1} include the endpoints, -3 and 1. This is expressed using closed interval notation: [-3,1].
Half-Open Interval
This type of interval includes only one of the endpoints of the inequality. For example, the set {x | -3 ≤ x < 1} include the endpoint -3. This is expressed using half-open interval notation: [-3,1)
Notations For Different Types of Intervals
We can follow certain rules and symbols to represent the interval notation for different types of intervals. Let us understand the different symbols that can be used to write a particular type of interval.
The symbol for Interval Notation
The notations we use for different intervals are:
- [ ]: This is a square bracket that is used when both the endpoints are present in the set.
- ( ): This is a round bracket that is used when neither endpoint is included in the set.
- ( ]: This is a semi-open bracket that is applied when the left endpoint is excluded and the right endpoint is included in the set.
- [ ): This is also a semi-open bracket that is applied when the left endpoint is in the set and the right endpoint is not in the set.
Interval Notation
Interval notation is a method to represent an interval on a number line. In other words, it is a way of writing subsets of the real number line. An interval comprises the numbers lying between two specific given numbers. For example, the set of numbers x satisfying 0 ≤ x ≤ 5 is an interval that contains 0, 5, and all numbers between 0 and 5.
Let us understand the interval notation and different types of intervals in detail using solved examples.
What is Interval Notation?
Interval Notation is a way of expressing a subset of real numbers by the numbers that bound them. We can use this notation to represent inequalities. We know an interval expressed as 1 < x < 5 denotes a set of numbers lying between 1 and 5.
Examples of Interval Notation
Suppose we want to express the set of real numbers {x |-2 < x < 5} using an interval. This can be expressed as interval notation (-2, 5).
The set of real numbers can be expressed as (-∞, ∞).
Different Types Of Intervals
Intervals can be classified based on the numbers the set comprises. Some sets include the endpoints specified in the notation, while others might partially or not include the endpoints. In general, there are three types of time intervals:
- Open Interval
- Closed Interval
- Half-Open Interval
Open Interval
This type of interval does not include the endpoints of the inequality. For example, the set {x | -3 < x < 1} does not include the endpoints, -3 and 1. This is expressed using open interval notation: (-3, 1).
Closed Interval
This type of interval includes the endpoints of the inequality. For example, the set {x | -3 ≤ x ≤ 1} include the endpoints, -3 and 1. This is expressed using closed interval notation: [-3,1].
Half-Open Interval
This type of interval includes only one of the endpoints of the inequality. For example, the set {x | -3 ≤ x < 1} include the endpoint -3. This is expressed using half-open interval notation: [-3,1)
Notations For Different Types of Intervals
We can follow certain rules and symbols to represent the interval notation for different types of intervals. Let us understand the different symbols that can be used to write a particular type of interval.
The symbol for Interval Notation
The notations we use for different intervals are:
- [ ]: This is a square bracket that is used when both the endpoints are present in the set.
- ( ): This is a round bracket that is used when both ends are not present in the set.
- ( ]: This is a semi-open bracket that is applied when the left endpoint is excluded and the right endpoint is included in the set.
- [ ): This is also a semi-open bracket that is applied when the left endpoint is included and the right endpoint is excluded in the set.
FAQs
Interval notation is a method to represent any subset of the real number line. We use different symbols based on the type of interval to write its notation. For example, the set of numbers satisfying 1 ≤ x ≤ 6 is an interval that contains 1, 6, and all numbers between 1 and 6.
When we represent the solution set of an interval on a number line, that is a graph for the interval notation.
We can graph the interval notation for a given set of numbers based on the type of number and specific symbols for the brackets used to enclose the set. This is because of its type.
The union “∪” symbol is used to denote the union of two or more intervals in any Interval notation. Interval notation is defined as the method used to represent any subset of the real number line.